C.4.4. Subroutines RSDF, RNDF, CHDF, CSDF, CNDF

PURPOSE

Factor a matrix into triangular form. Optionally perform forward reduction (and diagonal scaling) on right-hand side vectors.

SYNOPSIS

	CALL RSDF (LUA, LUF, LUB, LUX, NUMRHS)

	CALL RNDF (LUA, LUF, LUB, LUX, NUMRHS)

	CALL CHDF (LUA, LUF, LUB, LUX, NUMRHS)

	CALL CSDF (LUA, LUF, LUB, LUX, NUMRHS)

	CALL CNDF (LUA, LUF, LUB, LUX, NUMRHS)

INPUT PARAMETERS

LUA(25) = Integer Array.
File attributes for matrix [A].
LUF(25) = Integer array.
File attributes for the file where the matrix factors are to be written. These file attributes are usually the same as LUA to overlay the factored matrix on the original matrix to conserve space. If the original matrix is to be preserved, the FMSOM subroutine should be called to open the files for storing the matrix factors and create the LUF attribute list.
LUB(25) = Integer array.
File attributes for right-hand side vectors. If no forward reduction is performed during factoring, a dummy argument should be specified.
LUX(25) = Integer array.
File attributes for the file where reduced vectors are to be written. This parameter is usually the same as LUB to overlay reduced vectors on the original right-hand side vectors. If no forward reduction is performed during factoring, a dummy argument should be specified.
NUMRHS = Integer.
Number of right-hand side vectors to reduce during the factoring process. If NUMRHS is specified zero, no forward reduction (and diagonal scaling for symmetric matrices) is performed during factoring.

OUTPUT PARAMETERS:

None.

FMS PARAMETERS:

The following FMS Parameters are especially important to this routine:

Parameter	Description
	Input Parameters
IPRF	Factoring print code
IPRS	Solution print code
MDATAU	Call your subroutine to define or modify matrix data
NEQSUB	First equation of substructure
MPOSDF	Positive definite flag
MZERO	Zero pivot flag
NBITSZ	Number of lost bits on diagonal to call zero
NBITSP	Number of lost bits on diagonal to print a warning
RPIVOT	Value to set zero pivot reciprocal
PIVMIN	Absolute value of minimum pivot
IALGOR	Optional factoring algorithms
MINDIM	Minimum dimension to terminate Strassen's algorithm
IPOLLD	CPU synchronization on diagonal elements
	Output Parameters
NUMSCG	Number of diagonal sign changes during factoring
NPIVOT	Number of equations pivoted (SLAB format)
CONINV	Inverse condition number
ATERMS	Number of terms in matrix
AZEROS	Number of zero's in matrix
FZEROS	Number of zero's in matrix factor
SAVOPS	Number of floating point operations saved

DESCRIPTION:

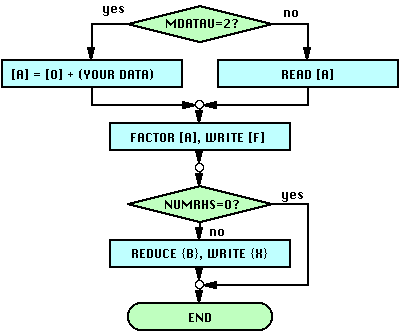
This subroutine performs the following steps:

Obtain [A]
If the FMS parameter MDATAU is 2, the matrix data is obtained by initializing [A] to [0] and calling one or more of the subroutines you provided to define the matrix data:

Matrix Format	Data Type	Matrix Symmetry	Subroutines Required
PROFLIE or BLOCK	Real	Symmetric	RSUBLK
PROFLIE or BLOCK	Real	Nonsymmetric	RSUBLK, RNUBLK
PROFLIE or BLOCK	Complex	Hermitian	CHUBLK
PROFLIE or BLOCK	Complex	Symmetric	CSUBLK
PROFLIE or BLOCK	Complex	Nonsymmetric	CSUBLK, CNUBLK
SLAB	Real	Nonsymmetric	RNUSLB
SLAB	Complex	Nonsymmetric	CNUSLB

If MDATAU has any value other than 2, the matrix is read from file LUA and your subroutine(s) are not called.

Factor [A]
The completed matrix [A] is then factored into one of the following forms:
[L][D][L]T = [A] for symmetric [A]

or
[L][U] = [A] for nonsymmetric [A].

Here, [L] is a lower triangular matrix with Lii = 1 and Lij = 0 for i<j. The matrix [D] is diagonal with Dij = 0 for i not equal to j. The upper triangular matrix [U] has nonzero values on and above the diagonal with Uij = 0 for i>j. The symbol "T" is used to denote the transpose for symmetric problems.
Write the factored matrix to file LUF.
FMS writes the matrix factors to the file you provide described by the attributes LUF. You may overwrite the matrix factors on the input matrix file LUA by specifying the same file attributes for LUF that you specified for LUA.
Reduce {B}
If you specified NUMRHS>0, FMS performs forward reduction (and diagonal scaling for symmetric problems) on the vectors in file LUB. This option saves reading the matrix factor [L] at the expense of rereading the right-hand side vectors {B} several times. If the number of solution vectors is small, or the solution vectors are in memory, this option should be used. However, if there are a large number of disk-based solution vectors, forward reduction should be performed using the solution subroutines RSDS, RNDS, CHDS, CSDS, CNDS. To skip this option, specify a zero value for NUMRHS and dummy arguments for LUB and LUX.

This subroutine is a subset of the more general assemble- factor subroutines RSDAF, RNDAF, CHDAF, CSDAF, CNDAF. It is equivalent to one of the following calls:


CALL RSDAF (LUA,1.0D0,NUMAI,IDUM,0,0,LUF,LUB,LUX,NUMRHS)

CALL RNDAF (LUA,1.0D0,NUMAI,IDUM,0,0,LUF,LUB,LUX,NUMRHS)

CALL CHDAF (LUA,1.0D0,NUMAI,IDUM,0,0,LUF,LUB,LUX,NUMRHS)

CALL CSDAF (LUA,1.0D0,NUMAI,IDUM,0,0,LUF,LUB,LUX,NUMRHS)

CALL CNDAF (LUA,1.0D0,NUMAI,IDUM,0,0,LUF,LUB,LUX,NUMRHS)

where IDUM is a dummy argument. The value of NUMAI is 0 if MDATAU = 2. Otherwise, NUMAI is 1. If you want to perform matrix factoring as a separate step, you may use this subroutine. Otherwise, you should use the more general assemble-factor subroutine.