PURPOSE
Assemble a global matrix and factor it into triangular form. Optionally perform forward reduction (and diagonal scaling) on right-hand side vectors.SYNOPSIS
CALL RSDAF (LUAI, ALPHA, NUMAI, LUS, NUMSF, LUA, LUF, LUB, LUX, NUMRHS)
CALL RNDAF (LUAI, ALPHA, NUMAI, LUS, NUMSF, LUA, LUF, LUB, LUX, NUMRHS)
CALL CHDAF (LUAI, ALPHA, NUMAI, LUS, NUMSF, LUA, LUF, LUB, LUX, NUMRHS)
CALL CSDAF (LUAI, ALPHA, NUMAI, LUS, NUMSF, LUA, LUF, LUB, LUX, NUMRHS)
CALL CNDAF (LUAI, ALPHA, NUMAI, LUS, NUMSF, LUA, LUF, LUB, LUX, NUMRHS)
INPUT PARAMETERS
- LUAI(25, NUMAI) = Integer array.
File attribute lists for input matrices used to initialize [A]. - ALPHA(NUMAI) = Real array (RS, RN, CH).
ALPHA(NUMAI) = Complex array (CS, CN).
Scale factors for input matrices. - NUMAI = Integer.
Number of input matrices. Specify 0 and dummy arguments for LUAI and ALPHA to initialize [A] to [O]. - LUS(25, NUMSF) = Integer array.
File attributes of each submatrix file. - NUMSF = Integer.
Number of submatrix files. If no submatrix files are used, specify 0 for NUMSF and a dummy argument for LUS. - LUA(25) = Integer array.
File attributes for the assembled matrix [A]. If the assembled matrix [A] is not being saved, specify 0. - LUF(25) = Integer array.
File attributes for the matrix factors. If no matrix factoring is required, specify 0. - LUB(25) = Integer array.
File attributes for right-hand side vectors. If no forward reduction is performed during factoring, a dummy argument should be specified. - LUX(25) = Integer array.
File attributes for the file where reduced vectors are to be written. This parameter is usually the same as LUB to overlay reduced vectors on the original right-hand side vectors. If no forward reduction is performed during factoring, a dummy argument should be specified. - NUMRHS = Integer.
Number of right-hand side vectors to reduce during the factoring process. If NUMRHS is specified zero, no forward reduction (and diagonal scaling for symmetric matrices) is performed.
OUTPUT PARAMETERS:
None.FMS PARAMETERS:
The following FMS Parameters are especially important to this routine:| Parameter | Description |
|---|---|
| Input Parameters | |
| IPRA | Assembly print code |
| IPRF | Factoring print code |
| IPRS | Solution print code |
| LOWASM | First changed equation |
| MDATAU | Call your subroutine to define or modify matrix data |
| NEQSUB | First equation of substructure |
| LUOK | Make a nonsymmetric matrix symmetric |
| MPOSDF | Positive definite flag |
| MZERO | Zero pivot flag |
| NBITSZ | Number of lost bits on diagonal to call zero |
| NBITSP | Number of lost bits on diagonal to print a warning |
| RPIVOT | Value to set zero pivot reciprocal |
| PIVMIN | Absolute value of minimum pivot |
| IALGOR | Optional factoring algorithms |
| MINDIM | Minimum dimension to terminate Strassen's algorithm |
| IPOLLD | CPU synchronization on diagonal elements |
| Output Parameters | |
| NUMSCG | Number of diagonal sign changes during factoring |
| NPIVOT | Number of equations pivoted (SLAB format) |
| CONINV | Inverse condition number |
| ATERMS | Number of terms in matrix |
| AZEROS | Number of zero's in matrix |
| FZEROS | Number of zero's in matrix factor |
| SAVOPS | Number of floating point operations saved |
DESCRIPTION:
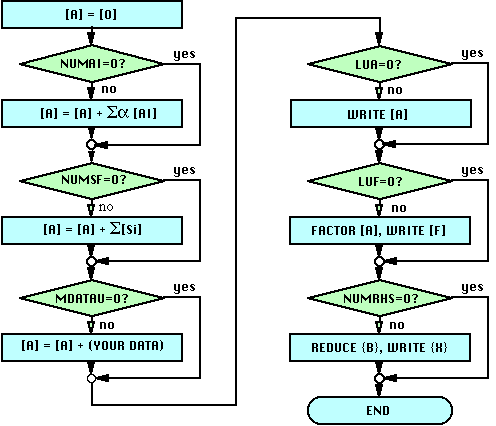This subroutine performs the following steps:
- [A] = [0]
The matrix [A] is initialized to [0]. Therefore only the nonzero coefficients need to be defined. - [A] = [A] +
SUM(ALPHA(i)*[AI](i)), m
Each of the initialization matrices LUAI(25,i) are scaled by their scale factor ALPHA(i) and added to the matrix [A]. The initialization matrices [AI] must have the same profile, symmetry, data type and record length as matrix [A]. This feature may be used for nonlinear or optimization analysis to initialize [A] to a previous value. For eigenvalue analysis, you may use the scale factor to shift the matrix. If you do not want to use initialization matrices, specify a 0 value for NUMAI and dummy arguments for LUAI and ALPHA. The FMS Parameter LUOK allows you to specify nonsymmetric matrices as input to the symmetric subroutines RSDAF and CSDAF. FMS averages the upper and lower triangle parts of the nonsymmetric matrix to make it symmetric. - [A] = [A] +
SUM([S]i), i=1,NUMSF
All of the submatrices on the files LUS(25,NUMSF) are then added to [A]. This assembly is typically used in finite element programs. You may skip submatrix addition by specifying a 0 value for NUMSF and a dummy argument for LUS. - Call your Subroutines
If the FMS Parameter MDATAU is set, one or more of the following subroutines you provide is called to define or modify [A].Matrix Format Data Type Matrix Symmetry Subroutines Required PROFLIE or BLOCK Real Symmetric RSUBLK PROFLIE or BLOCK Real Nonsymmetric RSUBLK, RNUBLK PROFLIE or BLOCK Complex Hermitian CHUBLK PROFLIE or BLOCK Complex Symmetric CSUBLK PROFLIE or BLOCK Complex Nonsymmetric CSUBLK, CNUBLK SLAB Real Nonsymmetric RNUSLB SLAB Complex Nonsymmetric CNUSLB - Write [A] to file LUA.
If LUA(1) is not 0, the assembled matrix [A] is written to file LUA. If you plan to factor the matrix and do not need to save [A], specify a zero value for LUA. - Factor [A]
The completed matrix [A] is then factored into one of the following forms:[L][D][L]T = [A] for symmetric [A]
or
[L][U] = [A] for nonsymmetric [A].
Here, [L] is a lower triangular matrix with Lii = 1 and Lij = 0 for i<j. The matrix [D] is diagonal with Dij = 0 for i not equal to j. The upper triangular matrix [U] has nonzero values on and above the diagonal with Uij = 0 for i>j. The symbol "T" is used to denote the transpose for symmetric problems.
If you do not want to perform matrix factoring, specify zero values for LUF(1) and NUMRHS and dummy arguments for LUB and LUX. FMS detects LUF(1)=0 and skips the rest of this subroutine.
- Write the factored matrix to file LUF.
FMS writes the matrix factors to the file you provide described by the attributes LUF. You may overwrite the matrix factors on one of the input matrices by specifying the same file attributes for LUF that you specified for one of the LUAI's. - Reduce {B}
If you specified NUMRHS>0, FMS performs forward reduction (and diagonal scaling for symmetric problems) on the vectors in file LUB. This option saves reading the matrix factor [L] at the expense of rereading the right-hand side vectors {B} several times. If the number of solution vectors is small, or the solution vectors are in memory, this option should be used. However, if there are a large number of disk-based solution vectors, forward reduction should be performed using the solution subroutines RSDS, RNDS, CHDS, CSDS, CNDS). To skip this option, specify a zero value for NUMRHS and dummy arguments for LUB and LUX.
If you are only performing matrix assembly and are not using initialization matrices (NUMAI = 0, LUF = 0, NUMRHS = 0), you may use the assembly subroutines RSDA, RNDA, CHDA, CSDA, CNDA.
If you are only performing matrix factoring and forward reduction (NUMAI = 0, NUMSF = 0) and you have not specific the matrix data with FMSROW or FMSCOL you may use the factoring subroutines RSDF, RNDF, CHDF, CSDF, CNDF.
These subroutines provide reduced argument lists when assembly and factoring are performed as separate steps.