C.3.6. Subroutines RSUBLK, RNUBLK, CHUBLK, CSUBLK, CNUBLK

PURPOSE

To provide a user interface for defining or modifying matrix data.
This is a subroutine you provide.

SYNOPSIS

SUBROUTINE RSUBLK (A, D, LOWEQ, LOCEQ, IROW1, IROW2, JCOL1, JCOL2, IJSTEP)

SUBROUTINE RNUBLK (A, D, LOWEQ, LOCEQ, IROW1, IROW2, JCOL1, JCOL2, IJSTEP)

SUBROUTINE CHUBLK (A, D, LOWEQ, LOCEQ, IROW1, IROW2, JCOL1, JCOL2, IJSTEP)

SUBROUTINE CSUBLK (A, D, LOWEQ, LOCEQ, IROW1, IROW2, JCOL1, JCOL2, IJSTEP)

SUBROUTINE CNUBLK (A, D, LOWEQ, LOCEQ, IROW1, IROW2, JCOL1, JCOL2, IJSTEP)

INPUT PARAMETERS

LOWEQ(*) = Integer array.
Matrix profile vector that specifies the lowest coupled equation for each equation. For the lower triangular matrix (RSUBLK, CHUBLK and CSUBLK), this is the column number of the first nonzero term in each row. For the upper triangular matrix (RNUBLK, CNUBLK), this is the row number of the first nonzero term in each column.
LOCEQ(*) = Integer array.
Base address for each equation (rows for RSUBLK, CHUBLK and CSUBLK; columns for RNUBLK and CNUBLK)
IROW1 = First row which can be changed
IROW2 = Last row which can be changed
JROW1 = First column which can be changed
JROW2 = Last column which can be changed
IJSTEP = Stride toward diagonal.

OUTPUT PARAMETERS

A(0:1) = Real array (RSUBLK and RNUBLK).
A(0:1) = Complex array (CHUBLK, CSUBLK and CNUBLK).
Matrix data array which is addressed by the {LOCEQ} vector.
D(*) = Real array (RSUBLK, RNUBLK and CHUBLK).
D(*) = Complex array (CSUBLK and CNUBLK).
Matrix diagonals.

FMS PARAMETERS

The following FMS Parameters are especially important to this routine:

Parameter	Description
MDATAU	Call this subroutine to define or modify matrix data

DESCRIPTION:

These subroutines, which are written by you, provide an interface to the FMS global matrix file. The RSUBLK, CHUBLK and CSUBLK subroutines define terms in the lower triangle and diagonal. The RNUBLK and CNUBLK subroutines define terms in the upper triangle and diagonal. For nonsymmetric problems (RN and CN), both the lower and upper subroutines are required.

To use this feature, FMS must be directed to call your subroutines. The MDATAU parameter provides this function. The default value of 0 results in skipping all calls to these subroutines.

When MDATAU is 1, FMS calls these subroutines during the assembly process. When MDATAU is 2, FMS calls these subroutines during the factoring process. If MDATAU is 1 or 2, these subroutines are called during the assembly-factor process.

If the entire matrix does not fit in memory, these subroutines are called several times. Each call defines a window of the matrix, bound by rows IROW1 through IROW2 and columns JCOL1 through JCOL2 as shown in the figure below. The diagonal can be defined during either or both calls.

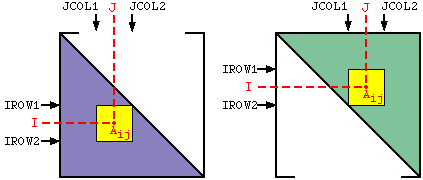
The location vector {LOCEQ} is used to address matrix data in the array A. For lower triangular terms (RSUBLK, CHUBLK, CSUBLK), the matrix coefficients are addressed as

A(I,J) = A(LOCEQ(I) + IJSTEP*J)

For the upper triangle terms (RNUBLK, CNUBLK), the matrix coefficients are addressed as

A(I,J) =  A(LOCEQ(J) + IJSTEP*I)

The row I ranges from IROW1 through IROW2 and the column J ranges from JCOL1 through JCOL2. The entire diagonal D, which is addressed as a single vector, is available during all calls.

The profile vector {LOWEQ} is passed to this subroutine so that you can check that no coefficients outside the matrix profile are being defined.

In general, these subroutines provide the best interface for finite difference, or general matrix formats. For finite element programs, the matrix assembly interface is more convenient.

FMS is distributed with user-supplied subroutines for populating test matrices with integer and random numbers. If your program supplies its own subroutines, they must be explicitly named on the link command to avoid using the subroutines supplied in the library.

Examples

As an example, suppose your program has a real nonsymmetric matrix C(100,100) in the common block MATRIX. The user supplied subroutines RSUBLK and RNUBLK would be as follows:

        SUBROUTINE RSUBLK (A, D, LOWEQ, LOCEQ,
     1  IROW1, IROW2, JCOL1, JCOL2, IJSTEP)
        COMMON/MATRIX/  C(100,100)
        INTEGER IROW1, IROW2, JCOL1, JCOL2
        INTEGER LOWEQ(IROW2), LOCEQ(IROW2)
        DOUBLE PRECISION A(0:0), D(1), C
        DO 20 IROW  =  IROW1, IROW2
           D(IROW) =  C(IROW,IROW)
           IF(IROW .LE. 1) GO TO 20
           LIEQ   =  LOCEQ(IROW)
           J2     = MIN0(JCOL2,IROW-1)
           DO 10 JCOL  =  JCOL1, J2
              A(LIEQ+IJSTEP*JCOL)  =  C(IROW,JCOL)
   10	      CONTINUE
   20	   CONTINUE
        RETURN
        END

        SUBROUTINE RNUBLK (A, D, LOWEQ, LOCEQ,
     1  IROW1, IROW2, JCOL1, JCOL2, IJSTEP)
        COMMON/MATRIX/C(100,100)
        INTEGER IROW1, IROW2, JCOL1, JCOL2
        INTEGER LOWEQ(JCOL2), LOCEQ(JCOL2)
        DOUBLE PRECISION A(0:0), D(1), C
        DO 20 JCOL  =  JCOL1,JCOL2
           IF(JCOL .LE. 1)  GO TO 20
           LJEQ   =  LOCEQ(JCOL)
           I2     = MIN0(IROW2,JCOL-1)
           DO 10 IROW  =  IROW1, I2
              A(LJEQ+IJSTEP*IROW)  =  C(IROW,JCOL)
   10      CONTINUE
   20   CONTINUE
        RETURN
        END

Note that for this example the profile vector {LOWEQ} is not used. It is assumed that the matrix is full.