Data Type

Integer

Default Value

2147483647 which is (231 - 1), a big number.

Description

This parameter modifies the factoring and solving processes to produce a reduced system of equations (substructuring). The new smaller system may be extracted, modified and solved.

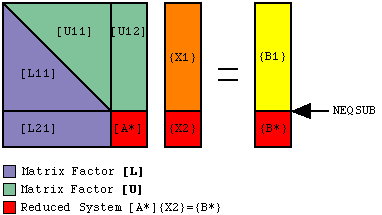
The parameter NEQSUB partitions the original system of equations 

   [A]{X} = {B}
as follows: 
   +-         -+ +-  -+   +-  -+
   | A11 | A12 | | X1 |   | B1 |
   +-----+-----+ +----+ = +----+<--NEQSUB
   | A21 | A22 | | X2 |   | B2 |
   +--   |    -+ +-  -+   +-  -+
For nonsymmetric problems, the matrix terms [A11], [A21] and [A12] are factored normally into [L11], [U11], [L21] and [U12]. However the matrix [A22]is only partially factored to produce the modified matrix [A*], 
   [A*] = [A22] - [L21][U12]   .
Similarly, during forward reduction the vector {B1} is reduced normally, but the vector {B2} is only partially reduced by 
   {B*} = {B2} - [L21]{B1}  .
The result is a reduced system of equations

NEQSUB Parameter Image

which may be solved for the solution vector {X2}. Once the solution vector {X2} is obtained, the values may be placed in the original vector {X} and FMS will complete the solution process for {X1}.

One important property of the reduced matrix [A*] and vector {B*} is worth noting. They are computed from the original matrix [A22] and vector {B2} by subtracting terms only. No multiplications on [A*] and {B*} have been performed. Therefore if you want to produce changes to the original terms in [A22] or {B2}, and those changes are in the form of additions or subtractions, they may be applied directly to the reduced system [A*] and {B*}.

The above strategy has some important applications which can save a considerable amount of computer time.

Design Optimization and Nonlinear Analysis

One application is in design optimization or nonlinear analysis where the system must be solved several times. Between each solution, some of the matrix coefficients in the lower right corner of the matrix are changed. Instead of completely resolving the entire system at each step, NEQSUB is first used to produce a reduced system containing the part of the matrix that changes. This smaller system is then used to find the optimal design or perform the nonlinear analysis. When the final solution is obtained, the values of {X2} are substituted back into the original system to compute {X1}. Note that the benefits of doing this depend on locating the changing matrix values in the bottom of the matrix.

Superelements

A second application is in building models of objects that have repeated sections. For example, suppose you want to analyze a ship that is constructed by repeating the same design down its length. You could first build a model of the generic section, numbering the equations so that the unknowns on the boundary were at the bottom of the matrix. The parameter NEQSUB could then be used to compute a reduced matrix [A*] which exactly represents the generic section in terms of the boundary unknowns only. The element assembly feature of FMS could then be used to assemble these generic sections into an overall model.

FMS contains some tools that can simplify this process. Subroutine RSDEX, RNDEX, CHDEX, CSDEX, CNDEX will extract the matrix [A*] from the original matrix file after factoring. Subroutine RSDANN, RNDANN, CHDANN, CSDANN, CNDANN will create a FMS matrix file from the extracted matrix [A*]. The regular FMS factoring and solving routines can be used to solve the reduced system.

Example

For further illustration on using NEQSUB to perform substructuring, refer to Example 7.