Overall Program Flow
FMS subroutines are divided into six groups, designed to match the 6 stages of your application program. |
|
FMS Subroutine Names
All FMS subroutines begin with the module name or "FMS". The data type and matrix symmetry determines which subroutine to use as follows:| Subroutine Name | Data Type | Symmetry |
|---|---|---|
| RSD... | Real | Symmetric |
| RND... | Real | Nonsymmetric |
| CHD... | Complex | Hermitian |
| CSD... | Complex | Symmetric |
| CND... | Complex | Nonsymmetric |
| FMS... | Both | All |
Calling Convention
FMS uses a standard FORTRAN calling convention. Actual parameters are passed by reference (address). Arrays are stored by rows first, then columns. For example A(2,2) is stored as {A11, A21, A12, A22}.You may call all FMS routines from C by passing addresses and noting that FORTRAN and C store arrays in the opposite order.
Character strings require special mention. The actual mechanics used to pass the address and length of character strings in FORTRAN varies by machine and compiler. A compiler option is usually required to match the FORTRAN interface. The current most popular FORTRAN interface is to pass the address of the character string in the normal position and append the value of the length of the string as an additional argument. When multiple character strings are passed, the length of each is appended in order.
Data Size
FMS stores the data as follows:- Real data is stored as 64-bit (8-byte) floating point numbers.
- Complex data is stored as a pair of 64-bit floating point numbers: first the real part then the imaginary part.
- On most machines, integers are stored as 64-bit (8-byte) integers. On older machines with 32-bit addressing operating systems integers are stored as 32-bit (4-byte) integers.
With this background, we are ready for a quick tour of the FMS subroutines, sorted according to the 6 stages of your analysis program.
1. Initialize FMS
| NAME | Function |
|---|---|
|
FMSINI FMSIN2 |
Initialize FMS - First Subroutine Called |
|
FMSIST FMSRST FMSCST |
Set an Integer Parameter Set a Real Parameter Set a Character Parameter |
|
FMSIGT FMSRGT FMSCGT |
Read an Integer Parameter Read a Real Parameter Read a Character Parameter |
|
FMSSET FMSSETC |
Set FMS Parameters interactively from FORTRAN Set FMS Parameters interactively from C |
-
CALL FMSINIREQUIRED:
The first FMS subroutine you call must be FMSINI. This subroutine initializes the FMS Parameters to default values and prints a description of the machine. You can only call FMSINI once during the execution of your program.It is strongly recommended that the call to FMSINI be the first executable statement in your program. On some systems this is required to intercept children processes that begin execution at the beginning of your program. In all cases, the timing information provided by FMS will be more meaningful if it includes the non- FMS part of your program.
-
CALL FMSIST(NAME,VALUE)OPTIONAL:
CALL FMSRST(NAME,VALUE)
CALL FMSCST(NAME,VALUE)
To change the values of integer, real and character FMS Parameters, call subroutines FMSIST, FMSRST, or FMSCST. -
CALL FMSIGT(NAME,VALUE)OPTIONAL:
CALL FMSRGT(NAME,VALUE)
CALL FMSCGT(NAME,VALUE)
You can obtain the value of integer, real and character FMS Parameters by calling FMSIGT, FMSRGT, or FMSCGT. -
CALL FMSSETOPTIONAL:
CALL FMSSETC
As an aid to software development, FMS includes subroutine FMSSET, which may be called to interactively view or alter FMS Parameters. You call FMSSET from FORTRAN or FMSSETC from C.
2. Open FMS Files
| NAME | Function |
|---|---|
| FMSOV | Open a Vector File |
| FMSOV2 | Open an Incore Vector File |
| FMSOS | Open a Submatrix File |
| RSDI RNDI CHDI CSDI CNDI |
Open General Matrix |
| RSDANN RNDANN CHDANN CSDANN CNDANN |
Open Full Incore Matrix |
| FMSOM | Open Second Matrix File |
| FMSBW | Compute Matrix Bandwidth |
| FMSPF | Compute Matrix Profile |
| FMSWF | Compute Matrix Profile from Wavefront Storage |
FMS organizes computation so once data is read from disk it is used many (often thousands) of times. This high "reuse" of data, which is possible with matrix algebra computations, allows FMS to match fast processing speed with slower disk transfer rates. FMS uses "asynchronous disk transfers" to overlap I/O with processing so data is available when required and buffered to disk after computation.
FMS uses three types of files for storing problem data:
-
Vector Files
Each file record holds one vector, whose length is determined by the problem size, data type and disk properties. Each vector file can hold multiple vectors. -
Submatrix Files
These files store matrix data as a collection of smaller matrices. Typically they are used by finite element programs. FMS includes the capability of assembling these submatrices into a global system matrix. -
Matrix Files
These files store a square array of data, which is partitioned into disk records. Three types of file formats are provided: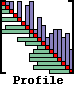
MFMAT=1: Profile Solver
Accounts for the sparsity of matrix [A] on an equation by equation basis. Typical applications include finite element and finite difference programs. This is the default for sparse matrices.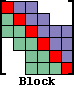
MFMAT=2: Block Solver
Divides the matrix [A] into square blocks, accounting for sparsity on a block by block basis. This solver uses industry standard BLAS3 kernels and provides excellent I/O performance on extremely large problems. Typical applications include boundary integral and moment method programs. This is the default for full matrices.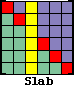
MFMAT=3: Slab Solver
Extends the functionality of the Block Solver by providing full column partial pivoting for full nonsymmetric matrices. You must explicitly set MFMAT to select this option.
- LUX(25), Vector File Attribute List
- LUS(25), Submatrix File Attribute List
- LUA(25), Matrix File Attribute List
2.1. Open Vector Files
A vector file "LUX(25)" is created in one of two ways:-
CALL FMSOV (NUMEQ,IDTYPE,NUMVEC,NAME,LUX)For vectors that will be stored on disk or FMS managed memory, call FMSOV. You should use this option if there are several vectors or permanent storage is required.
-
CALL FMSOV2(NUMEQ,IDTYPE,NUMVEC,X,LDX,LUX)If the size or number of vectors is small, and they are already stored in your application, call subroutine FMSOV2. FMS will create a "vector file" out of your storage so FMS can operate directly on your data. This eliminates any need to write or read this vector data to/from FMS.
2.2. Open Submatrix Files
A submatrix file "LUS(25)" is created by
CALL FMSOS(LENR,LENI,LENV,NUMVEC,NUMSUB,NAME,LUS)
Finite element programs that perform matrix assembly obtain the global matrix data from submatrix files. Subroutine FMSOS opens a submatrix file that includes storage for the submatrix and optional right-hand side vectors.
If you are using wavefront numbering, open a single submatrix file. The order that you write the data to the file determines the wavefront order.
If you generate submatrices by element type, you should try
and place each element type on a separate submatrix file.
When you open more than one submatrix file, you must store
the file attributes in the array
LUS(25, NUMSF),
where NUMSF is the number of submatrix files.
FMSOS is called NUMSF times, with the
attribute list LUS(1,I) supplied for the I-th submatrix file.
2.3. Open Matrix Files
A matrix file "LUA(25)" is created in one of three ways:-
CALL RSDI(LOWEQ,NUMEQ,NAME,LUA)Most applications should use these subroutines to create matrix files. The profile vector LOWEQ(NUMEQ) describes the sparsity of your matrix. As a special case LOWEQ(1)=-1 describes a full matrix.
CALL RNDI(LOWEQ,NUMEQ,NAME,LUA)
CALL CHDI(LOWEQ,NUMEQ,NAME,LUA)
CALL CSDI(LOWEQ,NUMEQ,NAME,LUA)
CALL CNDI(LOWEQ,NUMEQ,NAME,LUA)
-
CALL RSDANN(A,LDA,N,LUA)For full incore matrices A(LDA,N), use these subroutines to perform the combined function of creating the matrix file and writing data to the file. This interface is only recommended when you know the matrix will remain small. For a more general matrix file, use the previous method.
CALL RNDANN(A,LDA,N,LUA)
CALL CHDANN(A,LDA,N,LUA)
CALL CSDANN(A,LDA,N,LUA)
CALL CNDANN(A,LDA,N,LUA)
-
CALL FMSOM(LUA,NAME,LUF)Most applications overlay matrix factors on the original matrix to conserve space. However, if the original matrix is to be preserved, subroutine FMSOM may be called to create a second matrix file for storing the matrix factors.
2.4. Utilities for Opening Matrix Files
FMS includes the following utility subroutines which may be used to help create matrix files:-
CALL FMSBW(LOWEQ,NUMEQ,BWMAX,BWAVG,BWEFF)The FMSBW subroutine uses your profile vector LOWEQ(NUMEQ) to computes the maximum (BWMAX), average (BWAVG) and effective factoring (BWEFF) bandwidths of your matrix. You can use this information to determine matrix storage size and processing time.
-
CALL FMSPF(LUS,NUMSF,NEWNUM,MAXEQ,LOWEQ,NUMEQ)Subroutines FMSPF computes the profile vector LOWEQ(NUMEQ) from the information you wrote on the submatrix files LUS.
-
CALL FMSWF(LUS,NEWNUM,MAXEQ,LOWEQ,NUMEQ)Subroutine FMSWF converts the nicknames you wrote on the submatrix file LUS to equation numbers and computes the profile vector LOWEQ(NUMEQ).
3. Write Data to FMS Files
| NAME | Function |
|---|---|
|
FMSWRT FMSWR8 |
Direct access write to submatrix and vector files |
| FMSSWR | Sequential write to submatrix and vector files |
|
FMSEEK FMSEK8 |
Position file for sequential access |
|
FMSROW FMSCOL |
Write rows/columns to matrix file |
| FMSPUT | Write a block of data to a matrix or vector file |
| FMSCPY | Make a copy of a FMS file |
|
RSUBLK RNUBLK CHUBLK CSUBLK CNUBLK |
Define a block of matrix data |
|
RNUSLB CNUSLB |
Define a slab of matrix data |
3.1. Write Vector Files
Vector files are written as follows:-
CALL FMSWRT(LOGUNT,LOCUNT,ARRAY,NUMWRD)If you used FMSOV to open the vector file, transfer the vectors to FMS by calling FMSWRT to transfer each vector
ARRAY(NUMWRD)to fileLOGUNTstarting atLOCUNT. For example, the complex vectorsX(NUMEQ, NUMRHS)are transferred to FMS file LUX as follows:INTEGER LUX(25) COMPLEX*16 X(NUMEQ,NUMRHS) ... LDISK = 1 DO NRHS = 1, NUMRHS CALL FMSWRT (LUX(1), LDISK, X(1,NRHS), 2*NUMEQ) LDISK = LDISK + LUX(4) END DONote that the disk address begins at 1 and is incremented by the vector file record length, LUX(4). The number of words transferred, 2*NUMEQ, accounts for the real and imaginary parts of complex data.If the integers on your machine are only 32-bits, and your file is larger than 2 Gbytes, then you may pass the disk location to FMS as a 8-byte floating point number using subroutine FMSWR8.
- If you used FMSOV2 to open the vector file, the vector write operation is not required. FMS operates directly on the data in your program.
3.2. Write Submatrix Files
-
CALL FMSWRT (LOGUNT,LOCUNT,ARRAY,NUMWRD)Fixed length record submatrix files are written using FMSWRT. For example, submatrices in standard FORTRAN format are transferred to the fixed length record submatrix file LUS as follows:
INTEGER LUS(25) INTEGER IE(N+2), NELEQ, ITYPE IEQE(N) EQUIVALENCE (NELEQ, IE(1)) EQUIVALENCE (ITYPE, IE(2)) EQUIVALENCE (IEQE , IE(3)) REAL*8 S(N,N) ... NELEQ = N ITYPE = 1 LDISKR = 1 LDISKI = 1 NUMREC = LUS(5) DO NREC = 1, NUMREC ... ... fill arrays IEQE(N) and S(N,N) for record NREC ... CALL FMSWRT (LUS(1), LDISKR, S, N*N) CALL FMSWRT (LUS(2), LDISKI, IE, N) LDISKR = LDISKR + LUS(3) LDISKI = LDISKI + LUS(4) END DONote that the program increments the file addresses by the submatrix record lengths LUS(3) and LUS(4). These values were computed when you called FMSOS.If you are doing a nonlinear analysis and the model does not change, the submatrix integer file LUS(2) only needs to be written once.
If possible, you should store the submatrices on each file in the order of increasing lowest equation number. That is, write all submatrices that contribute to equation 1 first, followed by all remaining submatrices that contribute to equation 2, etc. This record order results in a minimum amount of data transfers during the assembly process. During development, the program can direct FMS to check the record order by including 1024 in the value of the IPRA parameter.
FMS buffers your write operations so the disk transfers can occur in parallel with your processing. The FMS Parameters LBUFSI, LBUFSR and LBUFSV control the size of the buffers used. If you are writing the records in a random order, you should turn off buffering by calling FMSIST, to set these buffer lengths to zero.
-
CALL FMSEEK(LOGUNT,LOCUNT)Variable length submatrix files are written sequentially using FMSSWR. The example above becomes:
CALL FMSSWR(LOGUNT,ARRAY,NUMWRD)
INTEGER LUS(25) INTEGER IE(N+2), NELEQ, ITYPE IEQE(N) EQUIVALENCE (NELEQ, IE(1)) EQUIVALENCE (ITYPE, IE(2)) EQUIVALENCE (IEQE , IE(3)) REAL*8 S(N,N) ... NELEQ = N ITYPE = 1 CALL FMSEEK (LUS(1), 0) CALL FMSEEK (LUS(2), 0) NUMREC = LUS(5) DO NREC = 1, NUMREC ... ... fill arrays IEQE(N) and S(N,N) for record NREC ... CALL FMSSWR (LUS(1), S, N*N) CALL FMSSWR (LUS(2), IE, N) END DO
3.3. Write Matrix Files
There are 5 ways to write data to FMS matrix files:-
CALL FMSROW(IEQN,DATA,LUA)These subroutines provide an easy interface when the matrix data is generated by rows or columns. You may also use this interface for Finite Element programs that perform their own assembly and store the data in profile (skyline) format. Each call transfers a row or column of DATA for equation IEQN to the FMS matrix file LUA. The data may be transferred in any row or column order. Either FMSROW or FMSCOL can be used. You may not mix calls to FMSROW and FMSCOL when filling a single matrix. After completing the calls to FMSROW or FMSCOL, you call RSDAF, RNDAF, CHDAF, CSDAF, CNDAF to factor the matrix.
CALL FMSCOL(IEQN,DATA,LUA)
-
Use submatrix addition.First you call FMSOS to open submatrix files. Then you use FMSWRT or FMSSWR to write the data to the submatrix real, integer and vector files. The submatrices may then be assembled as a separate step by calling RSDA, RNDA, CHDA, CSDA, CNDA, or during the factoring process with RSDAF, RNDAF, CHDAF, CSDAF, CNDAF. If you created submatrix vector files, they are assembled into global vector(s) using RSDAV and CSDAV
-
CALL FMSPUT(LUFMS, NROWS, NCOLS, IROW1, JCOL1, A(NROWS,NCOLS), LDA)This subroutine provides an interface when you generate the matrix data by blocks of size NROWS by NCOLS, starting at IROW1 and JCOL1 in the global matrix.
-
Set MDATAUThis option allows you to define or modify a window of the matrix by a subroutine you provide. FMS calls your subroutine as the matrix is being built.
For PROFILE and BLOCK matrices, provide one of the following:
SUBROUTINE RSUBLK (A,D,LOWEQ,LOCEQ,IROW1,IROW2,JCOL1,JCOL2,IJSTEP)These subroutines define a window of data in the lower triangle AL(IROW1:IROW2,JCOL1:JCOL2) and diagonal D(IROW1:IROW2).
SUBROUTINE CHUBLK (A,D,LOWEQ,LOCEQ,IROW1,IROW2,JCOL1,JCOL2,IJSTEP)
SUBROUTINE CSUBLK (A,D,LOWEQ,LOCEQ,IROW1,IROW2,JCOL1,JCOL2,IJSTEP)
For nonsymmetric matrices, also provide one of the following:
SUBROUTINE RNUBLK (A,D,LOWEQ,LOCEQ,IROW1,IROW2,JCOL1,JCOL2,IJSTEP)
SUBROUTINE CNUBLK (A,D,LOWEQ,LOCEQ,IROW1,IROW2,JCOL1,JCOL2,IJSTEP)
These subroutines define a window of data in the upper triangle AU(IROW1:IROW2,JCOL1:JCOL2).
If you are using the SLAB option for full column partial pivoting of full nonsymmetric matrices, provide one of the following:
SUBROUTINE RNUSLB (A,LOCI,LOCJ,LUFLAG,JCOL1,JCOL2,NUMEQ)
SUBROUTINE CNUSLB (A,LOCI,LOCJ,LUFLAG,JCOL1,JCOL2,NUMEQ)
to define the matrix data in the window (1:NUMEQ,JCOL1:JCOL2).
-
CALL RSDANN, RNDANN, CHDANN, CSDANN, CNDANNIf you used RSDANN, RNDANN, CHDANN, CSDANN or CNDANN to open a full incore matrix file, you do not need to write data to the matrix file. FMS operates directly on the data in your program.
4. Perform Matrix Algebra
| NAME | Function |
|---|---|
|
RSDAF RNDAF CHDAF CSDAF CNDAF |
Assemble and factor a matrix |
|
RSDA RNDA CHDA CSDA CNDA |
Assemble matrix |
|
RSDAV CSDAV |
Assemble vectors |
|
RSDF RNDF CHDF CSDF CNDF |
Factor a matrix |
|
RSUPIV CSUPIV |
Handle zero pivots. |
|
RSDS RNDS CHDS CSDS CNDS |
Solve |
|
RSDEX RNDEX CHDEX CSDEX CNDEX |
Extract a submatrix |
| FMSMM | Out-of-Core Multiply
[C] = [D] + [A][B],
|
|
RSDMVM RNDMVM CHDMVM CSDMVM CNDMVM |
Multiply {Y} = [A]{X} (FMSMM preferred) |
|
RSDSVM CHDSVM CSDSVM |
Multiply {Y} = SUM([Si]{X}) (FMSMM preferred) |
|
RNDVMM CNDVMM |
Multiply {Y} = {X}[F] |
|
RSDVVM CHDVVM CSDVVM |
Multiply [F] = {X}T{Y}, Symmetric [F] |
|
RNDVVM CNDVVM |
Multiply [F] = {X}T{Y}, General [F] |
|
RSDDVM CHDDVM CSDDVM |
Multiply [F] = {X}T[D]{X} |
|
RNDDVM CNDDVM |
Multiply [F] = {X}T[D]{Y} |
| FMSVAN | Vector Norms, Add, Subtract, Move |
| RSDWTP | Accumulate [S] = [S] + w[B]T[D][B] |
| RNDWTP | Accumulate [S] = [S] + w[B]T[D][A] |
-
Assemble, Fastor, Solve:
CALL RSDAF (LUAI,ALPHA,NUMAI,LUS,NUMSF,LUA,LUF,LUB,LUX,NUMRHS)These subroutines are the main workhorse of FMS. They perform the following tasks:
CALL RNDAF (LUAI,ALPHA,NUMAI,LUS,NUMSF,LUA,LUF,LUB,LUX,NUMRHS)
CALL CHDAF (LUAI,ALPHA,NUMAI,LUS,NUMSF,LUA,LUF,LUB,LUX,NUMRHS)
CALL CSDAF (LUAI,ALPHA,NUMAI,LUS,NUMSF,LUA,LUF,LUB,LUX,NUMRHS)
CALL CNDAF (LUAI,ALPHA,NUMAI,LUS,NUMSF,LUA,LUF,LUB,LUX,NUMRHS)
-
Initialize matrix [A] to
[0], or a linear combination of NUMAI input
matrices
[A] = SUM(ALPHA[AI])
- Add the submatrices specified on files LUS(25,NUMSF) to [A].
- If MDATAU is set, your subroutines are called to define or modify the matrix data.
- Optionally save the assembled matrix [A] on file LUA.
-
Factor the matrix and save it on file LUF.
Subroutines RSDAF, CHDAF and CSDAF factor the symmetric matrix [A] into the form[L][D][L] T = [A] (symmetric)
Subroutines RNDAF and CNDAF factor the nonsymmetric matrix [A] into the form
[L][U] = [A] (nonsymmetric)
- Perform forward reduction (and diagonal scaling for symmetric matrices) on NUMRHS vectors located on file LUB. Write the reduced vectors to file LUX.
-
Initialize matrix [A] to
[0], or a linear combination of NUMAI input
matrices
-
Assemble Matrix
CALL RSDA(LUS,NUMSF,LUA)If you want to perform matrix assembly as a separate step, use these subroutines. Note that they only assemble matrix data from submatrices LUS(25,NUMSF) and user supplied subroutines, as directed by MDATAU=1. If you wrote the matrix data using FMSROW or FMSCOL, you must call subroutine RSDAF, RNDAF, CHDAF, CSDAF or CNDAF to assemble and factor the matrix.
CALL RNDA(LUS,NUMSF,LUA)
CALL CHDA(LUS,NUMSF,LUA)
CALL CSDA(LUS,NUMSF,LUA)
CALL CNDA(LUS,NUMSF,LUA)
-
Assemble Vectors
CALL RSDAV(LUBI,LUS,NUMSF,LUB)If you wrote submatrix vector files, use these subroutines to assemble the submatrix vectors on files LUS(25,NUMSF) and add the results to the vectors on file LUBI. The resulting vectors are written to file LUB.
CALL CSDAV(LUBI,LUS,NUMSF,LUB)
-
Factor, Solve
CALL RSDF(LUA,LUF,LUB,LUX,NUMRHS)If you want to perform factoring as a separate step, use these subroutines. The matrix on LUA is factored and written to LUF. Optionally NUMRHS vectors on file LUB are reduced and written to file LUX.
CALL RNDF(LUA,LUF,LUB,LUX,NUMRHS)
CALL CHDF(LUA,LUF,LUB,LUX,NUMRHS)
CALL CSDF(LUA,LUF,LUB,LUX,NUMRHS)
CALL CNDF(LUA,LUF,LUB,LUX,NUMRHS)
-
Compute Pivots
SUBROUTINE RSUPIV(*,IEQN,A,S,D)If you want to perform your own zero pivot handling, set the FMS Parameter MZERO to 2 and provide one of these subroutines. This is almost never required.
SUBROUTINE CSUPIV(*,IEQN,A,S,D)
-
Solve
CALL RSDS(LUF,LUB,LUX,NUMRHS,ISKIP)The factored matrix on LUF is used to solve the NUMRHS vectors on LUB. The results are written to LUX.
CALL RNDS(LUF,LUB,LUX,NUMRHS,ISKIP)
CALL CHDS(LUF,LUB,LUX,NUMRHS,ISKIP)
CALL CSDS(LUF,LUB,LUX,NUMRHS,ISKIP)
CALL CNDS(LUF,LUB,LUX,NUMRHS,ISKIP)
The RSDS, CHDS and CSDS subroutines solve the following symmetric system:
[L][D][L]T{X} = {B} (symmetric)
The RNDS and CNDS subroutines solve the following nonsymmetric system:
[L][U]{X} = {B} (nonsymmetric)
These subroutines contain the formal parameter ISKIP, which can skip forward reduction (ISKIP=1) or back substitution (ISKIP=2).
-
Extract Submatrix
CALL RSDEX(LUA,A,LDA,N)If you are performing substructuring, use these subroutines to extract the substructure matrix A(LDA,N) from the lower-right corner of the FMS matrix LUA.
CALL RNDEX(LUA,A,LDA,N)
CALL CHDEX(LUA,A,LDA,N)
CALL CSDEX(LUA,A,LDA,N)
CALL CNDEX(LUA,A,LDA,N)
-
Matrix Multiply
CALL FMSMM(LUC,LUD,IACCUM,TRANSA,LUA,LUB)This subroutine performs one of the following matrix or vector multiply operations:
You may use these subroutines to compute the residual vector after solving a system of equations or in evaluating the quadratic form {X}T[A]{X} in an Eigenvalue analysis.Compute LUC and LUD IACCUM TRANSA LUA LUB {C} = {D} - [A]{B} {C} = [A]{B} {C} = {D} + [A]{B}Vector File -1
0
1'N' Matrix File Vector File {C} = {D} - [Si]{B} {C} = [Si]{B} {C} = {D} + [Si]{B}Vector File -1
0
1'N' Submatrix File Vector File {C} = {D} - {A}{B} {C} = {A}{B} {C} = {D} + {A}{B}Vector File -1
0
1'N' Vector File Vector File {C} = {D} - {A}T{B} {C} = {A}T{B} {C} = {D} + {A}T{B}Vector File -1
0
1'T' Vector File Vector File [C] = [D] - {A}T{B} [C] = {A}T{B} [C] = [D] + {A}T{B}Matrix File -1
0
1'T' Vector File Vector File -
Matrix-Vectors Multiply
CALL RSDMVM(LUA,LUX,LUY,NUMVEC,LUZ)These subroutines perform one of the following matrix [A] vector {X} multiply operations:
CALL RNDMVM(LUA,LUX,LUY,NUMVEC,LUZ)
CALL CHDMVM(LUA,LUX,LUY,NUMVEC,LUZ)
CALL CSDMVM(LUA,LUX,LUY,NUMVEC,LUZ)
CALL CNDMVM(LUA,LUX,LUY,NUMVEC,LUZ)
The matrix-vectors multiply calculation can be used to check the solution of the system of equations [A]{X} = {B}, or for iterative refinement {B'} = {B} - [A]{X}.Compute IACCUM {Y} = {Z} - [A]{X}-1 {Y} = [A]{X}0 {Y} = {Z} + [A]{X}1 -
Submatrix-Vectors Multiply
When the matrix [A] is generated by submatrices, it may be more efficient to perform the matrix-vector multiplication using the submatrices, rather than the assembled matrix [A].
CALL RSDSVM(LUS,NUMSF,LUX,LUY,NUMVEC,LUZ)
CALL CHDSVM(LUS,NUMSF,LUX,LUY,NUMVEC,LUZ)
CALL CSDSVM(LUS,NUMSF,LUX,LUY,NUMVEC,LUZ)
-
Vectors-Matrix Multiply
CALL RNDVMM(LUX,F,LUY,NUMX,NUMY,LUZ)
CALL CNDVMM(LUX,F,LUY,NUMX,NUMY,LUZ)
-
Vectors-Vectors Multiply
CALL RSDVVM(LUX,LUY,F,NUMXY)
CALL RNDVVM(LUA,LUY,F,NUMX,NUMY)
CALL CHDVVM(LUA,LUY,F,NUMXY)
CALL CSDVVM(LUA,LUY,F,NUMXY)
CALL CNDVVM(LUA,LUY,F,NUMX,NUMY)
-
Diagonal-Vectors-Matrix Multiply
CALL RSDDVM(LUX,LUD,F,NUMXY)The RSDDVM, CHDDVM and CSDVVM subroutines compute the quadratic form
CALL RNDDVM(LUX,LUD,LUY,F,NUMX,NUMY)
CALL CHDDVM(LUX,LUD,F,NUMXY)
CALL CSDDVM(LUX,LUD,F,NUMXY)
CALL CNDDVM(LUX,LUD,LUY,F,NUMX,NUMY)
[F] = {X}T[D]{X}
Only the lower triangle terms of the symmetric matrix [F] are computed and stored.
The RNDDVM and CNDDVM subroutines compute the full matrix as follows:
[F] = {X}T[D]{Y}
The results are stored in the array F(NUMX,NUMY).
-
Vector Norms, Add, Subtract, Move
CALL FMSVAN(LUX,IALPHA,LUY,INORM,RNORM,IOPT)
-
Matrix Triple Product
CALL RSDWTP(W,B,D,S,N,M)
CALL RNDWTP(W,B,D,A,S,N,M)
FMS includes subroutines for performing the following weighted matrix products:
[S] = [S] + W[B]T[D][B] (rsdwtp)
[S] = [S] + W[B]T[D][A] (rndwtp).
These calculations are typically used in finite element programs for integrating the element matrices.
5. Read Data from FMS Files
| NAME | Function |
|---|---|
|
FMSRED FMSRD8 |
Direct access read of vector file |
| FMSSWR | Sequential read of vector file |
| FMSGET | Read a block of data from a vector file |
CALL
FMSRED(LOGUNT,LOCUNT,ARRAY,NUMRED)
Most applications require only the solution vector {X}. Although submatrix and matrix data can be rewritten as part of a nonlinear analysis, the application program rarely reads it.
If you created the solution vector file by calling the FMSOV2 subroutine, the data is already in your program, and the read operation is not required. If you created the vector file by calling the FMSOV subroutine, the FMSRED subroutine is called once for each vector.
6. End FMS
| NAME | Function |
|---|---|
| FMSCV | Close a vector file |
| FMSCS | Close a submatrix file |
| FMSCM | Close a matrix file |
| FMSEND | End FMS - Last Subroutine Called |
-
CALL FMSCV(LUX)Whenever a vector file is no longer required, you may call FMSCV to close the file.
-
CALL FMSCS(LUS)Whenever a submatrix file is no longer required, you may call FMSCS to close the file.
-
CALL FMSCM(LUA)Whenever a matrix file is no longer required, you may call FMSCM to close the file.
-
CALL FMSENDREQUIRED:
The last call to FMS must be FMSEND. This subroutine shuts down all the FMS utilities and prints any requested reports. For the timings to have the most meaning, this call should be the last statement of your program.
Print Subroutines
| NAME | Function |
|---|---|
| FMSTIM | Obtain CPU and elapsed time |
| FMSPRV | Print vectors from vector file |
| FMSPRF | Print matrix from memory |
| FMSPRM | Print matrix from matrix file |
To obtain the CPU, Wall and I/O wait times,
CALL FMSTIM(LUX,NUMV1,NUMVEC,NMSG)
To print vectors from a FMS vector file,
CALL FMSPRV(LUX,NUMV1,NUMVEC,NMSG)
To print an array A(NROWS,NCOLS) in your program,
CALL FMSPRF(A,NROWS,NCOLS,ISTYPE,IDTYPE)
To print a matrix from a FMS matrix file,
CALL FMSPRM(LUA,NMSG)
Memory Management Subroutines
| NAME | Function |
|---|---|
| FMSIMG | Get Integer memory |
| FMSIMR | Return Integer memory |
| FMSRMG | Get Real*8 memory |
| FMSRMR | Return Real*8 memory |
| FMSCMG | Get Complex*16 memory |
| FMSCMR | Return Complex*16 memory |
CALL FMSIMG(IMD,LOC,LEN)
CALL FMSRMG(RMD,LOC,LEN)
CALL FMSCMG(CMD,LOC,LEN)
When you no longer require the storage, you can return it to the pool by calling
CALL FMSIMR(IMD,LOC,LEN)
CALL FMSRMR(RMD,LOC,LEN)
CALL FMSCMR(CMD,LOC,LEN)
If you want to list the contents of the FMS memory pool, you can include the statement
All memory in the FMS memory pool is automatically shared among the processors. If you plan to use the FMS parallel processing utilities (see below), you should use these utilities to store the data you want shared in the FMS memory management pool.Parallel Processing Subroutines
| NAME | Function |
|---|---|
| FMSPAR | Queue parallel tasks |
| FMSRUN | Start parallel tasks running |
| FMSYNC | Wait for parallel tasks to complete |
| FMSONE | Acquire mutual exclusive lock |
| FMSALL | Release mutual exclusive lock |
-
You begin be placing code that can run in parallel in a subroutine, which we will call
SNAME(P1, P2, ...). This code is written so that it is called
MAXCPU times, with each call performing part of the work.
Usually one of the NUMPAR parameters (P1, P2, ...) is different on each call so SNAME
will know which part of the work to do.
This subroutine may be tested in single processor mode as follows
DO ICPU=1,MAXCPU CALL SNAME(P1,P2,...) END DO - The above code is then modified to use
FMSPAR to run SNAME(P1,P2,...) in parallel.
FMSPAR is called (MAXCPU-1) times to place the work for each child process in a queue.
DO ICPU = 1,(MAXCPU-1) CALL FMSPAR(NUMPAR,SNAME,P1,P2,...) END DO - Subroutine FMSRUN is then called to start the children
running.
CALL FMSRUN - Subroutine SNAME(P1,P2,...) is called by the parent to do its part of the work.
CALL SNAME(P1,P2,...) - After the parent completes its work, it calls subroutine
FMSYNC
to wait for all the children to complete.
CALL FMSYNC
SUBROUTINE SNAME(P1, P2, ...,NTASKS)
INTEGER MYTASK
...
CALL FMSONE
MYTASK = NTASKS
NTASKS = NTASKS + 1
CALL FMSALL
The parent initializes NTASKS to 1. Each child then obtains a unique value of MYTASK that
can be use to perform its part of the work.
The FMS mutual exclusive lock FMSONE prevents two tasks from
reading and incrementing NTASKS at the same time.
This completes the quick tour of FMS subroutines. You may find more information about any subroutine through Appendix C, FMS Subroutines, available in the Table of Contents.