What Type of Problem Does FMS Solve?
Computers are used extensively in science and engineering to predict the behavior of products before they are built. The computer analysis helps in optimizing the design, improving performance and lowering cost.
The computerized analysis is based on the division of the problem into a large number of pieces. Within each piece, a model is built which describes the behavior of that piece. The individual pieces are then assembled together to form an overall model of the product.
As the number of pieces used to model the product is increased, the approximate solution obtained from the computer approaches the exact solution of the original problem. The maximum number of pieces that can be used, and therefore the accuracy of the analysis, is determined by the capacity of the computer hardware and software.
This modeling process is often called discretization, because the original problem is replaced by a finite number of discrete pieces. Analysis programs based on this approach include finite element, finite difference, boundary integral and moment method techniques. These formulations exploit the strength of digital computers, which perform large numbers of similar tasks rapidly.
Mathematically this simulation involves the solution of a large system of simultaneous equations
[A]{X} = {B}
where[A] is an N-by-N coefficient matrix that represents the product being analyzed,
{B} is an N-by-1 right-hand side vector that represents the environment that the product is operating in, and
{X} is an N-by-1 solution vector being computed, which represents the response of the product to the operating environment.
As the size of the matrix and vectors N is increased, the solution obtained by the computer approaches the exact solution of the problem.
What Limits N?
We want to make N as large as possible, so the computer simulation closely resembles the product. In order to understand what limits N, let us look at this process in more detail.The following flowchart illustrates the steps involved in performing this type of computer simulation.

|
1. Form [A] and {B} The process begins by forming local equations for each of the discrete pieces. These equations are in the form of contributions to the matrix [A] and right-hand side vector {B}. For large problems, this data is usually written to disk as it is generated.
2. Solve [A]{X} = {B}
3. Process solution {X} |
If the operating environment is severe, then the solution values in {X} will change the original model represented by [A] (nonlinear analysis). In addition, if the solution {X} indicates a bad product design, the process must be repeated (design optimization). In either case, a new matrix [A] is formed and the solution is repeated until convergence is obtained.
As we increase N, the time and storage requirements for Steps 1 and 3 increase differently than the requirements for Step 2. To illustrate this point, let us look at a model using a full complex nonsymmetric matrix [A] run on a computer operation at 100 Mflops. In this example, we assume that the time and storage requirements for Steps 1 and 3 are the same as Step 2 when N is 1000.
N is limited by processing time
As we increase N, the time required for Steps 1 and 3 increases between linearly and quadratically. If we use twice as many pieces it will take twice as long to compute their contribution. However for fully coupled problems the interaction of the pieces must be computed, introducing a quadratic component.
In Step 2, however, the scaling is drastically different. The time required to solve the system [A]{X}={B} increases as the cube of N. As a result, the maximum size of N on any computer is often limited by its floating point performance.
N is limited by storage requirements
Similarly, as we increase N the space required for storage by Steps 1 and 3 increase linearly. However, because [A] is an N-by-N array, the storage requirements for Step 2 increase as the square of N.The address space or storage capacity of a computer, memory or disk, can also limit the maximum value of N.
Modern computers use a hierarchical memory system, storing small amounts of data in high-speed registers close to the processor, working out to multiple levels of cache, memory and disk. Each level of storage offers more space but operates at a slower speed. If the data is not staged properly the performance will significantly degrade to the speed of the slowest storage device.
The Solution
Fortunately there are several things that can be done to solve the above problems and allow large values of N.Focus on [A]{X}={B}
The obstacles to increasing N listed above all occur in Step 2, the solution of [A]{X}={B}. Therefore we can focus on a well defined mathematical problem that is generic to all modeling techniques.Data Reuse
We noted above that the solution of [A]{X}={B} required N cubed operations on N squared pieces of data. As a result, each piece of data is "reused" N times. We can use this property to design special software that stages data from disk to memory, cache and registers. When accelerators are present, part of the data may also staged from memory to the accelerators. At each level of storage, the data is reused as much as possible. This reduces the total amount of data being transferred.Parallel Processing
Today's high speed computers contain multiple processors. By designing software to operate these processors in parallel, the time required for solution can be significantly reduced.Accelerators
Accelerators initially developed for graphic rendering have direct application for speeding up performance of matrix algebra. The large number of operations which can be performed in parallel can fully exploit these architectures.Disks
Storing data on disks costs about 100 times less than memory. In addition, disks may easily be added while memory is limited by the density of the memory chips and the number of memory sockets. Usually increasing memory requires replacing all the memory chips with those of a newer higher density.With proper algorithm design that stages data, the high reuse in matrix algebra allows the slower transfer of data from disk to be properly matched with processing at a significantly higher rate.
File Striping
When N is large, multiple disks will be required to store [A]. These disks can be operated in parallel to increase the rate at which data is transferred to and from memory.Asynchronous I/O
By default, when an application requires data from disk, processing is suspended until the data has been transferred. If the disks and processors are operating at the same speed, this can double the solution time.By developing special software to read data ahead of processing, data will be available when required by the processors. As a result, the disks and processors will run concurrently and no time will be lost waiting for data.
How FMS implements this technology
The solutions listed above all depend on special software. That is exactly what the Fast Matrix Solver (FMS) is designed to do.The following figure shows the original analysis program with the equation solution phase replaced by FMS.
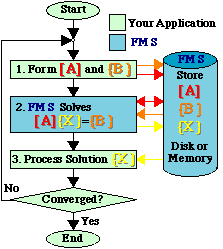
|
1. Form [A] and {B} FMS captures the matrix [A] and right-hand side vector {B} as they are generated. Parts of [A] may be transferred by rows, columns, blocks or finite elements. This data is stored directly in the FMS Database. Depending on the problem size, this database may physically reside in memory or on disk.
2. Solve [A]{X} = {B}
3. Process solution {X} |
Steps 1 and 3 of this analysis depend on the physics of the problem and the modeling technique used. Software and hardware efficiency are not a critical issue. By contrast, Step 2 is independent of the physics and modeling technique, but pushes the hardware to the limit. For this reason, FMS was designed from a hardware point of view.
There is an optimized version of FMS for most computer platforms. Each version makes maximum reuse of registers, cache, memory, accelerators (when available) and disks. Processors, accelerators and disks are operated in parallel to reduce runtime. On all systems, disks are operated in parallel and transfer data concurrently with processing.
While the internals of FMS are machine-specific, the interface to your application program is generic. This allows you to maintain a single version of your application while achieving peak performance on each computer system.
Wherever possible, FMS detects the available hardware and dynamically loads the supporting libraries as required. This allows you to maintain a single binary version of your application and run on a variety of hardware configurations.
FMS is High Technology Middleware
Today's computer industry consists of multiple vendors, with each vendor specializing in the products they produce. When you purchase a computer system, you are obtaining a product that was built by a team of specialists.
This team may be sorted by type of technology, hardware and software, as shown in the following figure:
| System Integrator They integrate the hardware and software into a system you can use. Also included is the operating system, which may be purchased separately. |
Applications These are programs that you either develop or purchase. They perform a specific function, from word processing to sophisticated scientific analysis. |
 |
|
| Chip Manufacturer Current fabrication technology requires extremely expensive facilities to produce the fast, high density processor and memory components of today's computers. Companies specialize in this technology, producing a variety of components for various system integrators. |
Middleware At the base technology level in software is an industry called middleware. This is software that is closely coupled to the hardware and performs a generic function to a variety of applications. Database software is a typical middleware product. |
FMS is middleware that combines database and math library functions. It extends the operating system by providing file striping, asynchronous I/O, memory management and parallel processing. FMS also interacts with the hardware at a low level with optimized kernels designed for each specific platform. When hardware accelerators are detected, they are automatically used to improve performance and reduce runtime.
Called as a library from programs written in FORTRAN or C, FMS provides a back door to the chip and operating system technology not normally available in programming languages. FMS may also be called from c++. In this case it is best viewed as a single managed object.
While the internals of FMS and its interface to the machine are constantly changing to take advantage of new technology, the application program interface has remained constant. This allows your applications to take advantage of new hardware technology with no development effort.
With today's world economy, maintaining a competitive advantage is critical. Products must continuously be refined to take advantage of new materials, manufacturing techniques and changing customer requirements. Computer simulations are well recognized as a vital ingredient in meeting these demands. By pushing the envelope of computer performance, FMS provides a technical advantage that helps you meet your goals.