DiskDrive

A key benefit of FMS is the ability to store the problem data on disk, which significantly lowers cost and extends the problem size. The most frequent question asked is how FMS can match the relatively slow transfer rates from disk with processors computing in the teraflop range. This section answers that question.

FMS may store data directly in memory, on solid state disk or on rotating disk. The choice may be made at runtime, depending on the size of the problem and storage available.

The storage used by FMS to build the matrix and vectors is usually temporary scratch storage, which is deleted after the job completes. Memory and volatile SSD meet this requirement. Non-volatile SSD and disks may also be used, with the files deleted after the job completes. Input problem data and results are usually stored on non-volatile media (disks).

FMS transfers data between disk and memory in large blocks, usually several Gbytes at a time. Large transfers provide the best possible performance including file striping, where several disks are operated in parallel to improve transfer rate.

The algorithms used by FMS are designed to write data once and reread it many times. This reduces wear on SSD and rotating disks. In addition, the read-transfer rate is usually faster than the write rate.

The choice of storage media is determined by cost and capacity. The following chart shows the storage cost options for full complex matrices up to 1,000,000 equations.

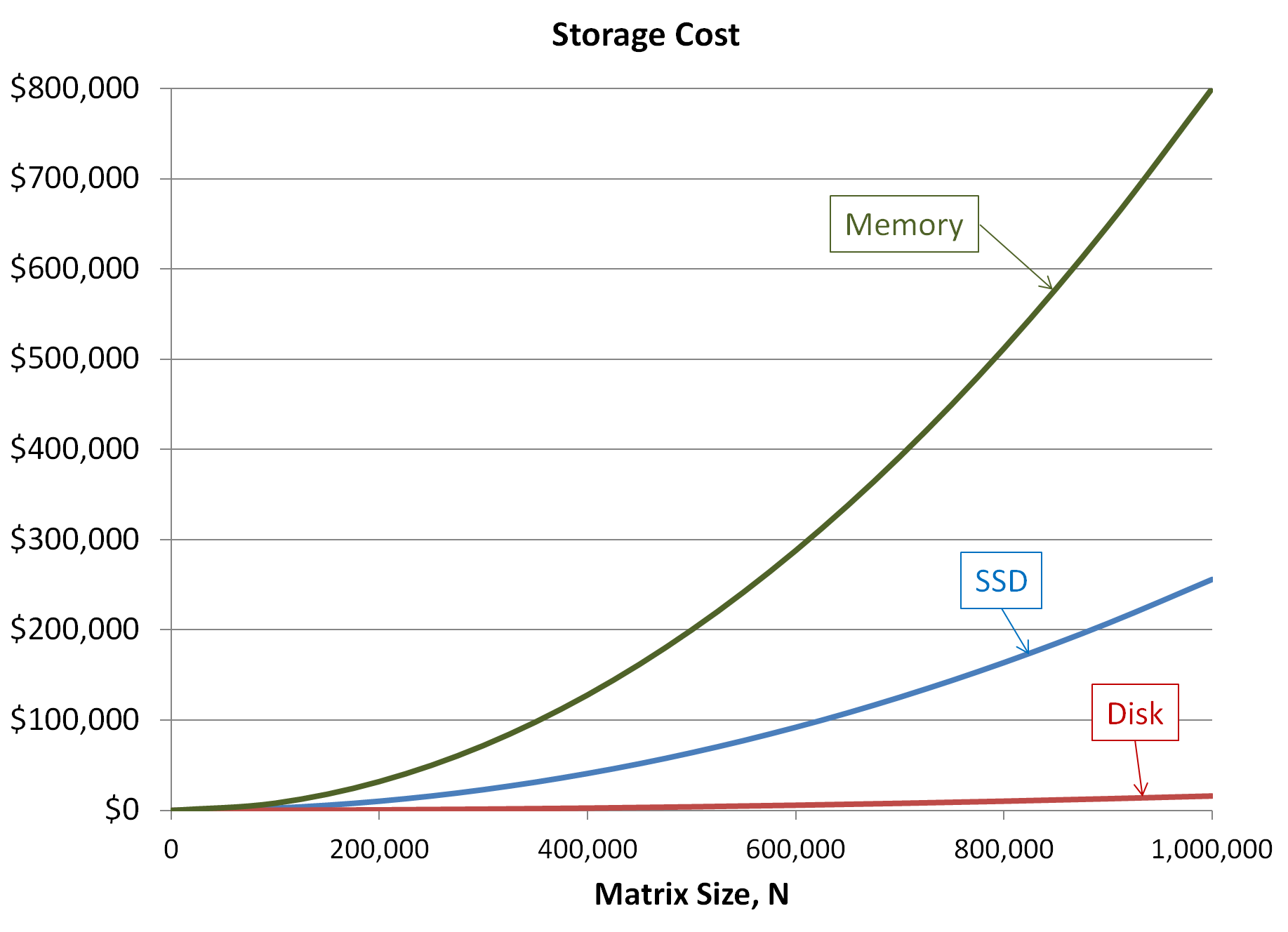
Storage Cost

For small problems, FMS may operate directly on data stored in memory. This storage may be in memory allocated by FMS or arrays in your application program.

As the problem size increases, a point is reached where direct storage in memory is not an option. The total amount of memory available is limited by the size of the memory stick and the number of memory sockets in the system. The memory size may also be limited by cost. A system fully populated with the latest memory sticks may cost up to an order of magnitude more than a system with minimal memory.

For larger problems, FMS offers the option of storing data on block-oriented devices including solid state or rotating disks. These devices provide significant cost savings over memory. More importantly they may easily be expanded to handle any problem size.

FMS transfers data between memory and disk in parallel with processing (asynchronous I/O). This allows the processors to run at full speed as if the entire data were stored directly in memory.

The key to matching slower disk transfer rates with fast processing rates is data reuse. If a piece of data is moved from disk to memory and used in 1000 calculations, then the disk transfer rate can be 1000 times slower than the rate required by the processors.

The amount of reuse required can be computed from the disk transfer rate, the compute rate and the amount of memory available.

Reuse

In order to balance slower disks with faster processing, data must be reused once it is transferred from disk to memory. If each word is reused 1000 times, then the disk transfer rate can be 1000 times slower than the processing rate.

The following example shows how FMS achieves the required reuse for balancing IO with processing.

The most frequent computation performed in FMS is the matrix multiply, as shown in the following figure:

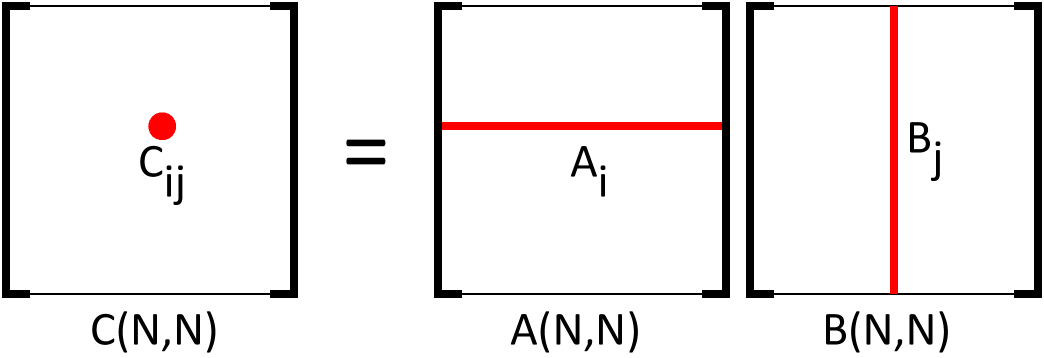
Matrix Multiply

Ci,j = N
Σ
k=1		 Ai,k Bk,j
To compute a single term in the output matrix Ci,j requires the dot product of a row of the first matrix Ai and a column of the second matrix, Bj. Each dot product requires N multiplies and N additions for a total of 2N floating point operations. Since [C] is an N by N matrix, there are N2 dot products to compute. Therefore the total number of floating point operations is 2N3.

For complex data, 4 times as much computation is required. The (real, imaginary) parts and their two cross products must be computed. Therefore to multiply complex matrices, 8N3 floating point operations are required.

Real Complex
Flops to multiply 2N3 8N3
The table summarizes the number of floating point operations required to compute a matrix multiply for both real and complex data types.

The matrix multiply will be used as part of a larger calculation where a sequence of M matrix multiplies are required. In that case, the output matrix [C] is updated M times as follows:

[C] = M
Σ
k=1		 [A]k [B]k

While one value of [C] is being computed we want to transfer in the next [A] and [B]. This requires 2N2 words for real data and 4N2 words for complex data.

Real Complex
Flops to multiply 2N3 8N3
Words to transfer 2N2 4N2
Reuse per word N 2N
The table summarizes the number of floating point operations required, the amount of data transferred and the number of times each data word is reused.

If the block size N being used for the matrix multiply is sufficiently large, then the desired reuse can be achieved to balance disk transfers with processing.

This property is used to stage data at all levels of the memory hierarchy. Optimized matrix multiply compute kernels use this property to stage data from memory to cache and then to registers. At each level a sub-block balances storage and processing speed.

IO/Compute Ratio

If we define the compute rate and transfer rate as
C=Compute Rate(Flops/sec.)
D=Transfer Rate(Bytes/Sec.)
then for double-precision 8-byte words the ratio of compute time to transfer time is given in the table.

Real Complex
Time to multiply (sec.) (2N3)/C (8N3)/C
Time to transfer (sec.) (16N2)/D (32N2)/D
IO/Compute Ratio ND/8C ND/4C

If the IO/Compute ratio is greater than 1, then the process will be compute bound and no time will be spent waiting for I/O to complete. The ratio gives the amount the computing can be increased without changing the I/O system.

If the IO/Compute ratio is less than 1, then the process will be I/O bound and time will be spent waiting for I/O to complete. In this case either the I/O performance (D) or the size of the matrices (N) transferred, or some combination of the two, should be increased.

Memory Required

Real Complex
N (IO/Compute Ratio=1) 8C/D 4C/D
Memory Reqired(bytes) 40N2 80N2
The amount of memory required can be computed from the size of the matrices being transferred, N. Storage must be provided for 5 matrices: [C], [A] and [B] being computed and the next [A] and [B] being transferred in. The table summarizes the memory requirements:

The amount of memory required for complex data can be shown as a function of the compute rate and disk transfer rate as follows:

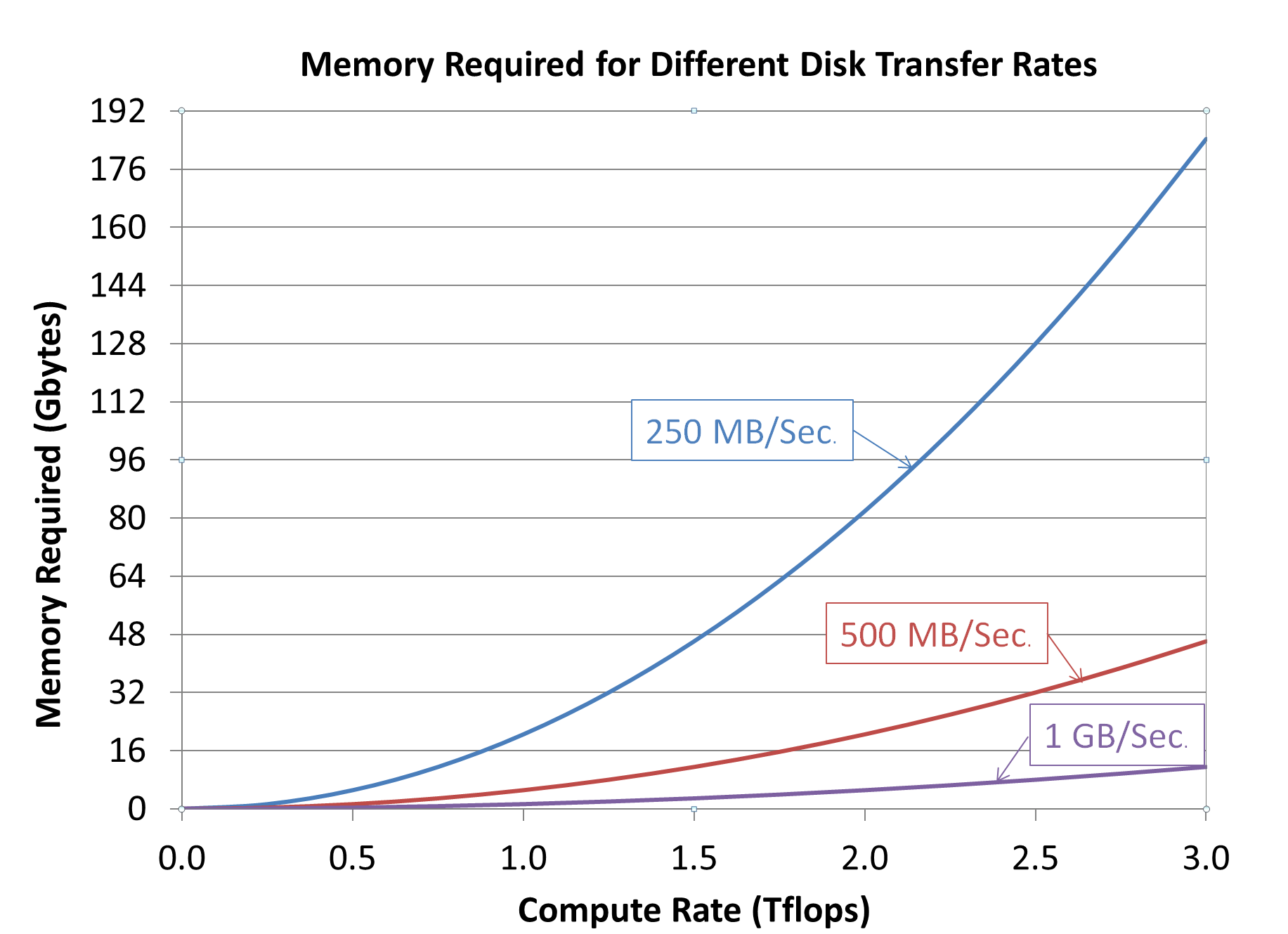
Memory Required

This chart shows the minimum amount of memory required by FMS to balance processing with I/O for complex data type. Twice this amount of memory is required for real data type. FMS automatically uses additional memory to reduce the number of I/O transfers performed. Some additional memory should be allowed for the operating system and problem data.

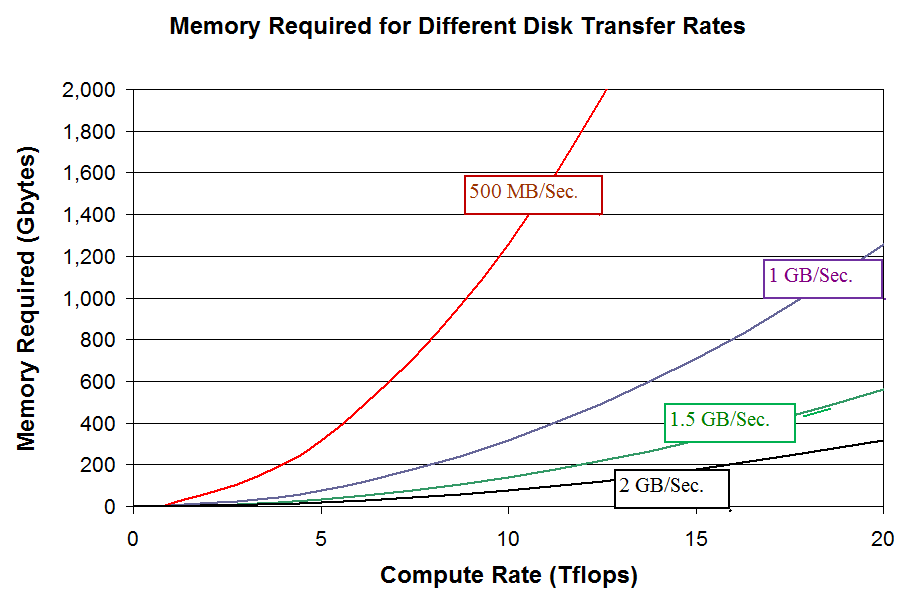Memory Required For faster systems, including servers with multiple GPUs, faster disks and more memory will be required. These systems are generally used for solving the largest problems, where multiple disks are available for striping. This provides the transfer rates required to keep memory requirements reasonable.