Welcome to Multipath's manual. Here you will find all the information necessary to incorporate FMSlib and Dashboard in your application, or run MatrixWarrior to test your hardware.

Your Application	Your Application	MatrixWarrior
Your Application	FMSlib	FMSlib
Dashboard	Dashboard	Dashboard
Hardware

This software collection consists of the following related products:

FMSlib, a matrix algebra library designed for optimum performance on large problems;
Dashboard, a performance analysis tool which generates a website on your computer showing hardware and performance information; and
MatrixWarrior, an application which uses FMSlib to test your hardware and Dashboard to display the results.

1. FMSlib

FMS (Fast Matrix Solver) is the industry standard for performing matrix algebra operations on large, dense matrices and groups of vectors. Packaged as a FORTRAN or C callable library, FMS may be incorporated into new or existing scientific and engineering programs to improve performance and provide large problem solving capability.

FMS Features

The primary function of FMS is to solve the following system of simultaneous equations:


[A]{X}  =  {B}

where:

[A] is an N-by-N coefficient matrix,

{B} is one or more right-hand side vectors,

{X} represents the solution vectors to be determined.

FMS offers the following significant developments that enable computers to sustain their maximum speed throughout the solution process:

FMS is based on mathematical formulations specifically designed to exploit parallel and pipeline architectures. All data structures and calculation sequences make maximum use of memory and arithmetic pipelines. This top-down approach to the development of FMS results in significantly better performance than can be obtained by performing local optimizations to existing algorithms.
FMS automatically takes advantage of parallel processing and GPU units when they are available.
FMS is designed from the machine's point of view. Where appropriate, performance-critical subroutines are coded directly in machine language. Maximum reuse is made of registers, cache and memory.
FMS performs data transfers to disks in parallel with processing. These asynchronous data transfers allow FMS to solve extremely large problems at maximum speed without requiring excessive memory.
FMS operates multiple disks in parallel to increase disk transfer rates (file striping).

FMS Modules

Storage and processing requirements depend significantly on matrix symmetry and data type, so FMS subroutines are divided into five modules, as shown in the following table:

FMS Subroutine Modules
MODULE	DATA TYPE	SYMMETRY	TYPICAL APPLICATION
RS	Real	Symmetric	Structural Analysis Heat Transfer
RN	Real	Nonsymmetric	Diffusion Fluid Mechanics
CH	Complex	Hermitian	Chemistry
CS	Complex	Symmetric	Radar Cross-Section Acoustics
CN	Complex	Nonsymmetric	Electromagnetics Circuit Design

Each module is optimized to provide maximum performance and minimum data storage for the type of problem it is designed to solve.

FMS Matrix Formats

FMS is actually 3 out-of-core solvers in 1:

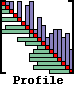
	PROFILE SOLVER: Accounts for the sparsity of matrix [A] on an equation by equation basis. Typical applications include finite element and finite difference programs.
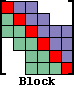
	BLOCK SOLVER: Divides the matrix [A] into square blocks, accounting for sparsity on a block by block basis. This solver uses industry standard BLAS3 kernels and provides excellent I/O performance on extremely large problems. Typical applications include boundary integral and moment method programs.
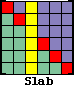
	SLAB SOLVER: Extends the functionality of the Block Solver by providing full column partial pivoting for full nonsymmetric matrices.

Because all 3 FMS solvers share the same application program interface, you may switch between solvers by simply changing a Parameter value, without recompiling or relinking your program.

Math Function Overview

FMS solves the system of simultaneous equations in two stages. First, the matrix [A] is factored into one of the following forms, depending on the symmetry of [A]:

Matrix Factoring
OPERATION	MATRIX SYMMETRY
OPERATION	SYMMETRIC	NONSYMMETRIC
MATRIX FACTORING	[L][D][L]^T = [A]	[L][U] = [A]

[L] is a lower triangular, [D] a diagonal, and [U] an upper triangular matrix. [L]^T is the transpose of matrix [L]. For Hermitian matrices, [L]^T will be used for the transposed conjugate of [L]. FMS uses data structures that permit the factors [L], [D], and [U] to be overlaid on the original matrix [A] to conserve memory and disk space.

Because factoring does not depend on the right-hand side vectors {B}, systems having multiple solution vectors are processed very efficiently. Compared to iterative methods, where all calculations must be repeated for each solution, this direct approach provides increased efficiency as the number of solution vectors increases.

If all the solution vectors are not known during the first solution, the factors may be saved and used later.

The second stage is to solve for the solution vectors {X}. This calculation is divided into the following steps:

Vector Solution
OPERATION	MATRIX SYMMETRY
OPERATION	SYMMETRIC	NONSYMMETRIC
FORWARD REDUCTION	[L]{Y} = {B}	[L]{Y} = {B}
DIAGONAL SCALING	[D]{Z} = {Y}	Not Required
BACK SUBSTITUTION	[L]^T{X} = {Z}	[U]{X} = {Y}

The first step is forward reduction, which computes the intermediate vectors {Y} from the right-hand side vectors {B} and lower triangular matrix factor [L]. The same calculation is performed for both symmetric and nonsymmetric matrices.

The second step is diagonal scaling. Because symmetric problems store only half the matrix, this calculation must be performed as a separate step. Nonsymmetric problems perform diagonal scaling during back substitution.

The final step is back substitution, which computes the solution vectors {X}. FMS permits the intermediate and solution vectors to be overlaid on the original right-hand side vectors.

In addition to solving simultaneous equations, FMS performs other matrix algebra operations. Included are matrix and vector multiply calculations typically used to compute Eigenvalues and Eigenvectors of the matrix [A].

The following matrix-vector multiply calculation multiplies one or more vectors {X} by a matrix [A] stored in FMS format:

{Y} = [A] {X}

The following vectors-vectors multiply calculation computes the inner products of groups of vectors and stores the results in the full matrix [F]:

[F] = {X}T {Y}

For diagonal matrices [D], FMS computes the quadratic form directly with the following equation:

[F] = {X}T [D] {Y}

FMS also provides for combining and scaling vectors with the vectors-matrix multiply operation:

{Y} = {X} [F]

Ease of Use

FMS is designed to be easy to incorporate into your application program. The following flowchart shows where FMS is interfaced to your application.

	Step 1: Matrix coefficients are transferred to the FMS Database as they are generated, by rows, columns, blocks or finite elements. FMS then assembles your data into matrix [A], which is stored in memory or on disk. Vector {B} may be transferred to FMS for storage, or FMS may be instructed to operate directly on the vector {B} in your program. Step 2: FMS solves the system of equations for the solution vector(s) {X}, which may be stored directly in your program or read from FMS. Step 3: Your application processes the solution vector(s) {X}.

Step 1:
Matrix coefficients are transferred to the FMS Database as they are generated, by rows, columns, blocks or finite elements. FMS then assembles your data into matrix [A], which is stored in memory or on disk. Vector {B} may be transferred to FMS for storage, or FMS may be instructed to operate directly on the vector {B} in your program.
Step 2:
FMS solves the system of equations for the solution vector(s) {X}, which may be stored directly in your program or read from FMS.
Step 3:
Your application processes the solution vector(s) {X}.

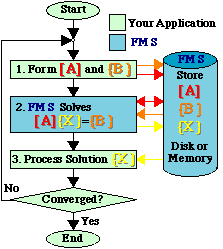
For nonlinear analysis, where the coefficients in matrix [A] depend on the solution values in {X}, the process is repeated until convergence is obtained. FMS contains special features to reduce the number of operations in step 2 when only some of the matrix coefficients are updated.

For most applications, the matrix [A] will far exceed the memory in the machine. Therefore the terms in matrix [A] must be transferred into the FMS Database as they are generated, rather than as a full array A(N,N).

Defining Matrix Data

Based on years of practical experience, the following options have been developed in FMS for defining matrix terms:

Rows or Columns
For applications which generate the matrix data by rows or columns, FMS includes the option to transfer each row or column as it is computed.
Finite Elements
FMS includes the matrix assembly phase of Finite Element programs. The element data is transferred to FMS as it is computed. FMS then assembles the global matrix.
Blocks
You may transfer sub-arrays of the matrix from storage in your application to the FMS database. Each call defines a window of the matrix. Only nonzero matrix terms need to be defined.
Full Matrix in Memory
For full matrices residing in memory, FMS includes subroutines which operate directly on your data.
Callback Subroutines
You may direct FMS to call subroutines you provide to define or modify the matrix data. Each call defines a window of the matrix.

In a Hurry?

If you are anxious to get started inserting FMS in your application, proceed as follows:

Skim over Chapter 3, "Installing FMS In Your Application Program". You will learn how FMS subroutines are organized and the role of FMS Parameters.
Skip to Chapter 5, "Examples of Using FMS". There is probably an example that is close to your application. Each FMS subroutine and Parameter referenced in these examples has been linked back to the detailed description. The source code is also available without the hyperlinks so you can compile and run the examples.

2. DASHBOARD

A Performance tool for your application

Dashboard is a performance-monitoring system that generates a website on your computer while your application is running. The generated site includes separate pages which provide detailed information on the CPUs, GPUs, Memory, Disks, File system, Software, a Call-tree and FMS Parameter values. Dashboard is easily installed in any application, even those that do not use FMSlib for matrix algebra.

You may use Dashboard in one of three ways:

Call Dashboard directly from your application;
Call FMSlib from your application, which is already instrumented with Dashboard; or
Run MatrixWarrior, which includes FMSlib and therefore also includes Dashboard.

For applications which use FMSlib, Dashboard includes a Performance page specifically designed for matrix algebra. This page shows the current state of the computation and the performance of critical hardware components. These reports may be linked to form a "movie" of the calculation. Multipath's Home Page contains a link to a movie produced by Dashboard.

3. MatrixWarrior

As libraries, FMSlib and Dashboard receive data from your application and drive the computer hardware. In order to demonstrate the performance of FMSlib and the displays available with Dashboard, a test application MatrixWarrior is included. This application generates matrix [A] and vector {B} according to your specifications. FMSlib then solves the system of equations [A]{X} = {B} for the solution {X}. Because MatrixWarrior is layered on FMSlib and Dashboard, all the features available in these libraries can be demonstrated by MatrixWarrior.

MatrixWarrior is an application that requires no programming. It can be used to:

Measure the actual performance and tune your machine(s);
Evaluate machines and options prior to purchase;
Tune and burn-in your machines after purchase;
Validate new machine designs before production;
Check possible hardware issues in production using a known application; and
Learn about the FMS and Dashboard libraries, which can be incorporated into your application to provide performance benefits and useful displays of information.

MatrixWarrior is available as a free download. Versions are available for Linux and Windows. Download MatrixWarrior to test your machine's performance and learn more about FMSlib and Dashboard.

1. Introduction